Ernesto Guisado's Website  » Articles  » Secure Random Numbers Articles | Miscellanea |

Secure Random Numbers

A variety of methods for generating and testing pseudo random number sequences.

Ernesto Guisado.
This material originally appeared in Windows Developer Magazine, copyright 2002, CMP Media.

Random numbers were once used mostly for mathematical applications like Monte Carlo Integration or for computer modeling and simulations. But in recent years the proliferation of security-related applications has increased the need for good random numbers. Examples are automatic password generation programs, session keys used in SSL/TLS-enabled web browsers, or random challenges in Kerberos. Online gambling is another example, as would be an attempt to automate the Lottery system. If you've ever generated a PGP public/private key pair you've also needed random numbers for it.

Generating random numbers for secure applications is a challenging task. In mathematical applications you only need to fool your simulation program and make it behave as if true random numbers had been used, but fooling the bad guys trying to cheat at your online poker parlor or preventing the NSA from reading your e-mail is going to be much more difficult.

In this article I explain how to generate secure random numbers on Windows. The source code that comes with the article includes several Visual C++ projects that highlight specific techniques and show how to use some freely available generators. I've also included some test programs and Perl scripts that you can use as a programmer's toolbox for random number generation. See the readme.txt file for details.

Randomness In the Machine

What I'm looking for is a way to generate a (sometimes very long) sequence of random numbers. Lehmer and others came up with a type of algorithm known as Linear Congruential Random Number Generator (LCRNG). This is the type of generator you'll find in the libraries that ship with your favorite programming environment; e.g., the rand function. Most of them look like this: 

static long y = seed; 
long rand() { 
  y = (a*y + c) % m; 
  return y; 
}

Where a, c and m are fixed constants (normally prime numbers fulfilling certain mathematical properties), y has to be initialized with a "seed" value. The formula is simple and deterministic. Run it a million times with the same values for a, y, c and m and you'll always get the same sequence. Computer algorithms used to generate random sequences are called "pseudo random number generators" (PRNGs).

Testing for Randomness

The "pseudo random" part in PRNG means they are not really random—it just looks random. To distinguish between good and bad generators, people have come up with increasingly elaborate tests that a PRNG has to pass in order to be considered good. Later on, I'll show some very comprehensive test suites that you can run on your PRNG to assess it. Other tests are simpler but easy to implement and, therefore, useful as an internal sanity check. There are some simple tests as specified in the NIST FIPS 140-1 U.S. Federal Standard:

If we're really serious about testing RNGs, we have several programs at our disposal. I normally use ENT, DIEHARD and the NIST Test Suite.

ENT

John Walker is the author of ENT: A Pseudorandom Number Sequence Test Program. ENT implements five simple tests. The main limitation is that the tests all work on byte-sized chunks and therefore might miss multibyte patterns in the sequence. The main advantage is that it is fast, easy to run and easy to understand. It has a useful additional option (ent -c) that lets you see the individual frequencies for each byte. The frequencies should be evenly distributed.

DIEHARD

George Marsaglia's DIEHARD Test Suite is very complete and has been used by companies such as RSA to evaluate their cryptography products. The test suite includes around 14 tests. A description is included with the program and makes an amusing read: not only because of the funny names (e.g., the Parking Lot test) they have but also because they seem surprisingly convoluted. Most of them return a p-value that should be in the range [0,1]. Occasional values could be near 0 or 1. For a very bad sequence you might see a p-value like 1.000000 or .00000. The main limitations of DIEHARD are that you need to generate an input file that's around 15-MB long to get all the tests to run and that the evaluation of the results isn't easy. I recommend running DIEHARD on some known bad generator first, so that you get used to seeing what bad values look like.

NIST

The mother of all test suites is the Statistical Test Suite from the National Institute of Standards and Technology that's used to evaluate cryptographical applications. It comes with an extensive PDF file describing how it works. A summary is available in an ITL Bulletin. The NIST test suite is made up from 16 different statistical tests that are described in the documentation.

This test suite is distributed in source code and currently only works on Solaris. I hacked the code just enough to make it compile with Visual C++ and have included the program (assess.exe) with the article. Once you get it running, the main problem is that each test seems to require some parameters, and no defaults are provided. Once I figured out the right parameters, I found the results (found in the finalAnalysisReport file) quite easy to interpret.

Breaking LCRNGs

It turns out LCRNGs are problematic even for non-security related applications: the graph of a LCRNG shows a regular lattice structure when analyzed using high dimensions. Several authors came up with ways use this regularities to break LCRNGs after seeing only a short sequence of values.

Particularly scary was an article by Bellare, Goldwasser and Micciancio called "Pseudo-Random" Number Generation within Cryptographic Algorithms: the DSS Case (1997), Lecture Notes in Computer Science. The Digital Signature Standard (DSS) signature algorithm requires the signer to generate a new random number with every signature. Using an LCRNG as generator makes DSS so weak that the system can be broken after seeing only three signatures.

Another common problem with simple linear congruential generators are a short period and the fact that the low order bits are frequently much less random than the high order bits. The short period can be a problem if you need to generate random numbers very fast which is true in applications like Kerberos. M.J.B. Robshaw pointed out that a PRNG working at 1 MByte/sec and with a 232 period (typical for simple LCRNG) will repeat itself after only 29 seconds (8.5 minutes). This isn't acceptable for crytpographical purposes.

Pure Crypto PRNGs

Cryptanalysis, the art and science of breaking ciphers and recovering encrypted messages, deals mostly with pattern analysis. Written text shows patterns and redundancies that can be used to recover the original text from the encrypted version. Modern cryptographic algorithms (see Sidebar 1) such as DES, RC4 or AES have been designed to defeat this kind of pattern analysis. Their output looks totally random. Passing statistical tests for randomness is expected from any respectable crypto algorithm.

The simplest cryptographic PRNG is probably the one specified in the ANSI X9.17 standard for Key Generation. This standard is mainly used to generate DES keys for banking applications. X9.17 is based on the Triple-DES encryption algorithm, but could be used with any symmetric block cipher (e.g., the new AES). Before you start you'll need a secret seed and a secret key. As primitives you only need Triple-DES and exclusive-OR. 

block seed = SecretValue();
key k = SecretKey();
block out;
while (NeedMore()) {
  block t = 3Des(k, DateTime());
  out = 3DES(k, t^seed);
  seed = 3DES(k, t^out);
  // use out
}

Each time we need to generate a random 64-bit value, we encrypt the current time, XOR it with the current internal state, and encrypt the result. This result is the output of the PRNG. We also XOR the output with the encrypted timestamp and use it as new internal state for the next iteration. This PRNG is quite slow (because 3DES is slow) but secure.

The source code I've provided includes a VC++ project (see listing x917gen.cpp) that uses the X9.17 implementation in Wei Dai's Crypto++ to produce random output for analysis.

Breaking crypto PRNGs

Now let's imagine I want to break X9.17. Where would I start? Perhaps some examples of people breaking other PRNGs might help as inspiration.

Quite notorious is the case of the Texas Hold'em Poker, which was broken by a group from Cigital. They knew a lot of details about the code in question because the shuffling algorithm was actually made public. The people at Cigital discovered that the program used a LCRNG and that the seed was based on the number of milliseconds since midnight. The people at Cigital didn't need to break the LCRNG: there are only 60,000 milliseconds per minute. If you can guess the clock of the machine that's doing the shuffling (give or take one minute), you'll only have to check around 180,000 possibilities (3 minutes). They waited until several cards had been dealt and then they searched through all the possibilities to see which one produced the known set of cards.

Another similar case was the Netscape browser problem. Even though the PRNG that Netscape used was more secure than the one I just discussed, it still made a serious mistake: The seed was based on the process ID and the current time. Both values are quite easy to guess for somebody who can access the same machine (e.g., on UNIX). Goldberg and Wagner published a nice article in Dr. Dobbs Journal exposing this weakness.

A final example comes from the Strip automated password generator for PalmOS. A description of the problem and a C program to demonstrate it was posted to the excellent SecurityFocus.com mailing list. Strip uses an LCRNG to generate each character of the password. Does the posted code exploit this weakness? No. There is an easier way: due to a bug, the LCRNG is seeded with a 16-bit variable. This means there are only 65,536 possible starting values for the password generation. This is easy to implement as exhaustive search!

From these experiences it looks like the most likely venue of attack against X9.17 would be to guess the secret password and the secret seed. All the strength of Triple-DES won't save you if you use your license-plate number as secret key! But relying on some user providing a good initial password is just avoiding the responsibility. Also, if the the password gets compromised, the whole system breaks down. We need a way for a deterministic program to generate some "true" randomness that can be used to generate the initial keys. That way the program can automatically change the key from time to time to protect it. This process of making up the random starting values is known as "entropy collection" or "entropy gathering".

Entropy

Imagine somebody flipping a coin. Heads or tails? How much information do you have to guess? Claude Shannon called this quantity entropy, uncertainty, or information content. Each coin flip has two possible outcomes and each of them is equally probable: heads or tails? 0 or 1? According to Shannon, each toss has 1 bit of entropy. If each outcome has the same probability, you just need to take the log2 of the number of possible outcomes:

Here's a script to calculate it given the number of outcomes and how many times you want to repeat the experiment: 

use strict;
sub log2 {
  my $n = shift;
  return log($n)/log(2);
}
my $use = 
  "entropy.pl nsymbols length\n";
my $nvals = shift or die $use;
my $len = shift or die $use;
my $ent = log2($nvals ** $len);
print "Max entropy: $ent\n";

So if you need a totally random 56-bit DES key and want to generate it with a dice, you'll need to roll it 22 times!

If the probability of each outcome is different (e.g., loaded dice), you say that the output is biased. This means that there is less entropy, because it is easier to guess. I won't bore you with the formula, but here is a Perl script to calculate it given the probability of each outcome: 

use strict;
sub log2 {
  my $n = shift;
  return log($n)/log(2);
}
my $use = 
  "entropy.pl 0.6 0.4\n";
my $h;
for (@ARGV) {
  my $p = $_;
  $h += $p*log2($p)
}
$h *= -1;
print "Shannon Entropy H=$h";

Shannon's formula tell us that a coin toss that has probabilities of 0.75 and 0.25 for heads and tails, only has 0.8 bits of entropy in it. That means we need more coin tosses to get the same level of security.

Another problem is correlation. That is, when one outcome depends on the previous outcomes. Something is considered random if there is no bias and no correlation. This is important because source of entropy may be both biased and with correlations. We'll need to find a way to get around this problem.

Sources of entropy on Windows

A lot of software sources of entropy rely on using high-precision timers to record when some external "random" event happened. A good start is therefore to get the highest precision timer you can get you hands on. Normal GetTickCount returns values in milliseconds and you should not trust it to be more accurate than 10 ms. A better approach is to use the QueryPerformanceCounter API that normally has a frequency of 1.1927 MHz. The return value tell us if the system supports high-performance counters. QueryPerformanceCounter returns a 64-bit value that you could use directly using the __int64 data type. Most of the time, I only need the 32 least-significant bits, because they are the ones that keep changing. In that case I can avoid using __int64 and do it like this: 

unsigned long query() {
  LARGE_INTEGER time;
  QueryPerformanceCounter(&time);
  return time.LowPart;
}

Now if you're really into low-level stuff you might know Pentium processors have a read timestamp counter (RDTSC) instruction that returns a counter that gets incremented with the processor clock. On my (already old) machine I get 350 MHz. Here's some inline assembly to get it's value: 

// pentium read time stamp counter
typedef unsigned __int64 uint64;
uint64 rdtsc() {
  uint64 t;
  __asm rdtsc
  __asm mov dword ptr[t],eax
  __asm mov dword ptr[t+4],edx
  return t;
}

Now that I've got a good high-resolution timer, what should I measure? The user can be a good source of random events: Some people recommend measuring keystroke frequency, time between mouse clicks, and mouse position. Most available PRNGs have source code that shows how to do this.

Without a user, things get trickier. The main approach seems to be to take snapshots of some rapidly changing system data in the hope that it should be hard for somebody to reproduce, even if he has access to the machine.

Most people seem to use ToolHelp32 on 95 and performance registry data on NT. According to the Windows SDK, a ToolHelp32 snapshot is a read-only copy of the current state of one or more of the following lists that reside in the system's memory: processes, threads, modules, and heaps. On NT, the HKEY_PERFORMANCE_DATA registry key allows access to the raw NT performance counters.

Timing the arrival of a network packets is also a popular variant, as is using APIs to get the value for the foreground window, the last window message processed, and other rapidly changing values.

Yet another approach is timing scheduler related events that depend on rapidly changing details, like the number of threads currently running on the machine and on low-level OS events arrivals.

Estimating entropy

Inspired by a simpler program in the book Building Secure Software (by John Viega and Gary McGraw, Addison-Wesley, 2002), I've written a C program called "countbits" that divides a file into 1-, 2-, 3-, 4- and 8-byte chunks and counts the frequencies of the individual bits (see Listing 2). If you start seeing bits with 100% or 0% frequency, you know that they aren't changing at all, which means there is no entropy in them. Ideally you would like to see lot's of near 50% values (indicating no bias). There could still be the possibility of a correlation; e.g., you could be writing 0x00 and 0xFF alternatively, which would mean perfect 50% (as each bit continuously alternates between 1 and 0); but still no real entropy. On the other side seeing values like 75% also doesn't mean there isn't any randomness in the source.

Random sequences should be hard to compress. You can quite easily get an upper bound on the entropy content of our entropy sources by compressing them with some compression utility. If you compress your entropy source by 50%, you're quite sure that there aren't more than 4 bits of entropy per byte.

There isn't much theory in this area and being very conservative still seems like the best strategy. As an example the Yarrow PRNG never believes there is more than a 50% of entropy in any input, no matter what you tell it.

Entropy Distillers

Now the design behind X9.17 looks a bit clearer: Apart from the secret seed and key, the only randomness going into it is the timestamp value. But how much of the timestamp is hard to guess for somebody trying to break my system? Certainly not the year, perhaps the minute? Second? Millisecond? As we saw when estimating entropy, this is hard to tell. The designers applied a 3DES operation to the timestamp before using it. This "spreads" the entropy evenly across the whole 64-bit block. This way they don't have to worry about which bits in the timestamp contain more entropy.

In general you're better off by taking the whole timestamp or whatever entropy input you're using and mixing the bits using a strong hash function. This should remove any bias and correlation in the input. Most entropy pools work by hashing the current contents of the pool with whatever new values you want to throw into it. This way the entropy accumulates in the pool. Given enough time the contents of the pool will have good entropy (but never more that the length of the pool).

This gives us all the building blocks we need for a good PRNG.

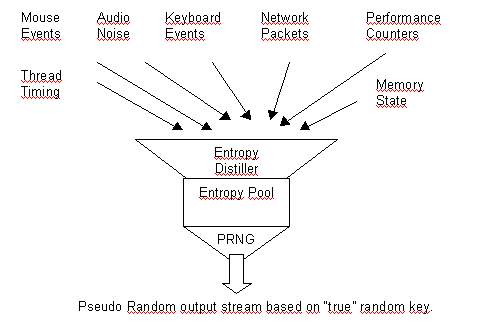
Building blocks for a good PRNG

  1. Several independent entropy sources.
  2. An entropy pool where the entropy is distilled and accumulated using a strong cryptographic hash function.
  3. A X9.17-like PRNG that uses the contents of the pool as key and generates as much pseudo-randomness as the user wants.

Implementors seem to vary in how they value these steps. The designers of Yarrow maintain steps 1 and 2 are really only needed to recover from key compromise. On the other side, Peter Gutmann seems to think that if steps 1 and 2 are properly implemented, you don't really need step 3. He calls step 3 "stretching" the random data.

Using CryptGenRandom

Microsoft's Cryptography API (CAPI) supplies a function called "CryptGenRandom" that retrieves data from a strong PRNG. Here's an function that generates random long values using CryptGenRandom: 

#define _WIN32_WINNT 0x0400
#include <windows.h>
#include <wincrypt.h>

long getrand()
{
  HCRYPTPROV hProv = 0;
  CryptAcquireContext(&hProv, 
    0, 0, PROV_RSA_FULL, 
	CRYPT_VERIFYCONTEXT);
  long rnd;
  CryptGenRandom(hProv, 
  	sizeof(rnd), (BYTE*)&rnd);
  CryptReleaseContext(hProv, 0); 
  return rnd;
}

How does the CAPI generator work internally? There seems to exist some difference of opinion. Peter Gutmann claims it uses SHA-1 as hash. On the other side Michael Howard and David LeBlanc, authors of Writing Secure Code (Microsoft Press Books, 2002), and the documentation of the Windwows CE version of the API, claim that MD4 is used.

CAPI claims to use a combination of low-level system information, the current process ID, the current thread ID, ticks since boot, current time, various high-precision performance counters and memory information. All this information is added to a buffer, which is hashed using MD4 and used as the key to modify a buffer, using RC4, provided by the user.

Another MS document also says that PRNG implementors should periodically generate a new seed to avoid placing too much reliance on the PRNG. It would be hard to believe if they hadn't followed this advice themselves.

Intel RNG

Some of Intel's PIII CPU's come with a hardware RNG based on sampling the thermal noise in resistors. It uses SHA-1 as mixing function for the outputs. It also runs some FIPS 140-1 autotests.

Once you've downloaded the drivers from Intel's site, you can use it using Microsoft's CAPI. Only the call to CryptAcquireContext needs to be changed: 

  HCRYPTPROV hProv = 0;
  CryptAcquireContext(&hProv, 0, 
	  INTEL_DEF_PROV, 
	  PROV_INTEL_SEC, 0);

Some people consider this the ultimate solution. Others are afraid because all the entropy comes from one source (albeit a good one). If your PIII has the Intel RNG, I would at least use it as additional source of entropy.

Yarrow

Yarrow uses one of the nicest designs I've seen. See http://www.counterpane.com/yarrow.html for a full description. It uses a fast pool and a slow pool using SHA-1. Several entropy sources feed into these pools. The PRNG output is generated using Triple-DES with a secret key. The pools are used to change the key in case it has been compromised. The fast pool makes the secret key change frequently, but perhaps doesn't add much entropy. The slow pool changes the key very infrequently, but very conservative entropy estimates make sure that the generated key is very secure. The key is also changed from time to time by using some of the Triple-DES output.

The Yarrow source code uses a previous design. It maintains a single SHA-1 context as entropy pool and from time to time updates a secret state that is passed through SHA to produce the output. It uses mouse and keyboard hooks to generate entropy. A ToolHelp32 snapshot is also used on 95 and HKEY_PERFORMANCE_DATA on NT.

Interesting is that two independent estimates are maintained for each entropy source: the one provided by the programmer and another one based on compressing using zlib and dividing by 2. The minimum of both is used.

Yarrow is implemented as a DLL with a front end that has to be run as user program. Shared memory is used to maintain a common entropy pool.

Tiny/Egads

Egads is an evolution of Yarrow. It is multiplatform and works as service on Windows 2000 and XP. I submitted some patches to make it work on NT 4, so we might find support for that platform in later releases. The current version is Alpha Release 0.7.1, and while writing this article I found some problems that I reported to the authors.

The best (only) description of the Tiny design is currently in the book Building Secure Software. It says that Tiny uses the UMAC message authentication code instead of a traditional cryptographic hash to process inputs and AES in counter mode to protect outputs. Unsurprisingly, it also uses a slow pool similar to Yarrow's to seed the PRNG.

Egads also uses the performance data snapshot approach. But it uses Allen Denver's Performance Data Helper (pdh.dll) instead of the native NT registry access. Egads also gets entropy from the time it takes to call Sleep(0) 10,000 times. Each Sleep call tells the thread scheduler that we're ready to yield the processor. Here's some example code using our rdtsc function: 

uint64 sleeptime() { 
  uint64 a = rdtsc();
  for (int i=0; i < 10000; i++)
    Sleep(0);
  return rdtsc()-a;
}

Timing thread-creation code with the RDTSC instruction or even with the QueryPerformanceCounter output results in something that to my eyes looks pretty random already: 

unsigned 
__stdcall 
thread(void*) { 
  _endthreadex(0);
  return 0;
} 

void createandwait() { 
  HANDLE th;
  unsigned id;
  th = (HANDLE)_beginthreadex(
    0, 0, &thread, 0, 0, &id);
  WaitForSingleObject(th, 
    INFINITE);
  CloseHandle(th);
}

Egads does this in the UNIX version, but in a loop that repeats 100 times. For some reason the Windows version doesn't use it.

Truerand

Another similar approach is used in the NT version of librand, a random number package based on event interval variations, from Matt Blaze, Jack Lacy, and Don Mitchell. The basic idea behind the NT version of truerand is to create a thread that increments a counter in a tight loop while the main program sleeps for a specified amount of time (16 ms in the implementation I've seen). Bits 0..2, 3..5 and 6..8 are xor-ed together with the result from the previous thread creation to yield 3 more-or-less random bits. This process is repeated 11 times to give a total of 33 bits. 32 bits of those are returned as random long value. For additional security, two 32-bit values are processed together with SHA and only the first byte of the result is used as output.

This generator is very slow and I couldn't generate enough output to run the tests on it (only ENT), but the raw output (before SHA post-processing) already looked promising.

I've included the truerand sources with the article source code in a VC++ project called "librandgen" that you can use to generate random data to analyze it.

Cryptlib

Peter Gutmann's cryptlib has a very elaborate PRNG called "continuously seeded pseudorandom number generator" (CSPRNG) which combines some very elaborate entropy gathering code with a big entropy pool that's stirred using SHA. The output of the pool is used to seed a X9.17 generator that produces the final output. The whole thing is even more complex and is described in Gutmann's 1998 Usenix Security Symposium paper "The generation of practically strong random numbers".

Cryptlib has a fast and a slow system snapshot. The slow snapshot is the system-snapshot approach that other PRNGs also use. Interesting is the fast snapshot, as Gutmann has managed to collect an impressive list of frequently changing API functions. Examples might be the GetMessagePos API that returns "the point occupied by the cursor when the last message retrieved by the GetMessage function occurred" or the GetOpenClipboardWindow function that "retrieves the handle of the window that currently has the clipboard open".

Cryptlib also uses the Intel PIII RNG as additional entropy source and includes extensive internal checks (based on FIPS 140-1) to detect problems during entropy collection.

Crypto++

Wei Dai's nice Crypto++ library supports a generic entropy pool based on PGP's randpool.c, and uses SHA as mixing function. This is implemented using class RandomPool. Due to the support for crypto primitives build into the library, the random pool code is less than 100 lines of straightforward C++. Crypto++ also includes an implementation of a variant of X9.17 (see class X917RNG) and a wrapper around the MS CAPI (class NonblockingRng).

The version I've examined (Crypto++ 4.2) doesn't seem to include any entropy gathering code.

BeeCrypt

A special mention must be given to the entropy gathering code in the BeeCrypt crypto library, written by Bob Deblier of Virtual Unlimited. This library includes code that uses the waveform-audio input functions in mmsystem.h to read the noise on the soundcard microphone port. Because they use the asynchronous waveInOpen API, this entropy source uses up very little CPU. Like most good entropy sources it is pretty slow in collecting, but you can't have everything.

The BeeCrypt entropy collector also includes a simple internal check to detect if things go badly. From what I've seen in the code, there is no strong mixing function involved, only a simple deskewing algorithm to get rid of any bias in the output. This means statistical test should be a good indication of the real entropy content. I wrote a VC++ program (beecryptgen.cpp) to write out a 15-MB entropy data file using the beecrypt DLL. No test complained. A hex dump of the file reveals no obvious patterns and the bit count looks like this: 

Counting for 8 bits
Bit 0: 978039 = 49.95%
Bit 1: 979145 = 50.01%
Bit 2: 978801 = 49.99%
Bit 3: 978753 = 49.99%
Bit 4: 979989 = 50.05%
Bit 5: 978585 = 49.98%
Bit 6: 978880 = 50.00%
Bit 7: 979202 = 50.01%

BeeCrypt also includes another entropy collector that tells the user to type random stuff on the console and finds entropy in the time between keystrokes. It uses QueryPerformanceCounter as the timing function.

Getting entropic data is done through the quite simple to use entropyGatherNext function. They only nitpick is that I found it quite bizarre that a environment variable is used to specify which entropy source you want to use! The source code for the article contains a VC++ project called "beecryptgen" that you can use to try out BeeCrypt.

OpenSSL

The 0.9.6c version of the OpenSSL engine includes a random number generator that can be easily accessed: 

#include <openssl/rand.h>

// ...
unsigned char rnd[2500];
RAND_pseudo_bytes(rnd,
  sizeof(rnd));

The Windows version seems to use CAPI to get random data from the MS PRNG and from the Intel PRNG. It also uses the system-snapshot approach and additionally mixes in a screen snapshot. The user key presses and mouse movement are also used, but you have to call RAND_event explicitly.

The timing function is particularly interesting because it seems to support detecting RDTSC and downgrading gracefully to QueryPerformanceCounter or even GetTickCount if the higher resolution version isn't available.

While the entropy collection code is quite clean and supports entropy estimates, I found the pool management code to be quite messy. It maintains a large pool (1K) and stirs it by applying a hash function to each hash-sized chunk. It does this each time something gets added to the pool. It also maintains some counters that get mixed in with the rest of the information.

Although you can call the entropy gathering code from outside (using RAND_poll), this function only seems to be used once internally at initialization time. This doesn't look like a good idea as it remains the responsibility of the user to add randomness to the pool using RAND_seed and RAND_add.

Finally, a good thing about OpenSSL is that the source code includes a file called "randtest.c" that implements the FIPS 140-1 tests.

Other PRNGs

PGP and the GNU Privacy Guard (GnuPG) also include entropy gathering code, but I didn't include them because the code is there to support the program itself and not as general purpose PRNG.

Finally, if you're using Java or C# you can use built-in classes that give access to secure random numbers. Java has a class called java.security.SecureRandom for this purpose, and the .NET Framework has System.Security.Cryptography.

Conclusions

If you want an easy way out, use Microsoft's CAPI. It is quite secure and you can always enhance it by collecting your own entropy and feeding it into CryptGenRandom. Another simple option (when available) is the Intel hardware RNG, which you can use through the same interface.

If I wanted to use something where I have the source code, and if I was happy with the licensing conditions (free for open source and for low-income closed source programs), I would definitely use Peter Gutmann's cryptolib. Yarrow's design is good and Egads/Tiny looks promising, but current implementations are nowhere near the level of functionality provided by cryptlib.

Finally if I wanted to roll my own, I would use Crypto++'s RandPool and X917RNG classes to do the groundwork for me and use CAPI, Intel, and BeeCrypt's Audio noise as additional sources of randomness.

Resources

Along with the other web sites mentioned in the article, there are several great RNG resources on the net. I'll also maintain an updated list of resources at http://triumvir.org/rng: